数字特性法,顾名思义,就是利用数字的特性来做题。主要包括奇偶特性、整除特性、以及比例倍数特性。数字特性法是最能体现行测特点的方法,效率极高。本文重点介绍其中的奇偶特性。
关于奇偶特性的基本内容就不在本文中赘述,下面主要阐述奇偶特性在数量关系中的运用。
一是当知差求和或者知和求差时可考虑采用奇偶特性。
例:某次测验有50道判断题,每做对一题得3分,不做或做错一题倒扣1分,某学生共得82分,问答对题数和答错题数(包括不做)相差多少?( )
A.33 B.39
C.17 D.16
问答对题数和答错题数之差,而根据题中“某次测验有50道判断题”可知答对题数与答错题数之和为偶数,根据奇偶特性中的“和差同类”,可知两者之差也必为偶数。快速排出A、B、C,锁定答案为D。
二是当题中提到所求项或相关项与2的倍数的关系时,可考虑采用奇偶特性
例:有8个盒子分别装有17个、24个、29个、33个、35个、36个、38个和44个乒乓球,小赵取走一盒,其余各盒被小钱、小孙、小李取走,已知小钱和小孙取走的乒乓球个数相同,并且是小李取走的两倍,则小钱取走的各个盒子中的乒乓球最可能是( )。
A.17个,44个 B.24个,38个
C.24个,29个,36个 D.24个,29个,35个
由题中“已知小钱和小孙取走的乒乓球个数相同,并且是小李取走的两倍”可知小钱取走的乒乓球必为偶数,快速排出A、C。将B、D中的任意一项代入即可。将B代入,小钱取走的乒乓球数为62,因此小李取走的乒乓球数为31,而题中八个盒子的数量不管如何组合,都不可能组合成31。矛盾。排除B。因此本题选项为D。
三是当题目需要考虑多个整数之间的关系但缺少充分条件时,可以考虑采用奇偶特性。
以2010年4月25日联考第14题为例。第A、B、C、D、E是5个不同的整数,两两相加的和共有8个不同的数值,分别是17、25、28、31、34、39、42、45,则这5个数中能被6整除的有几个?
A. 0 B. 1 C. 2 D. 3
由“两两相加的和共有8个不同的数值”其中两两加和必有重复的数值。我们能确定的有:(假设A<B<C<D<E﹚A+B=17①,A+C=25②,C+E=42③,D+E=45④。若能知道B+C或者C+D,那我们就可以求出A、B、C、D、E。我们将目的定为求出B+C(当然也可以锁定为求出C+D)。因此我们需要将B和C联系起来。①-②得:C-B=8.根据奇偶特性,可得C+B必为偶数,要么为28,要么为34。又因为B和C分别为第二小和第三小的数,两者之和必定为比较小的那个数,为28。将B+C=28⑤与A+B=17①,A+C=25②联立求解,解得A=7,B=10,C=18。从而也可以解出D=21,D=24。因此这五个数中能被6整除的有2个。
更多精彩资讯请关注查字典资讯网,我们将持续为您更新最新资讯!
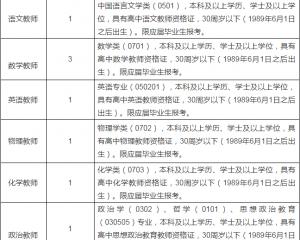 江西师范大学附属中学2020年招聘教师2020-06-24
江西师范大学附属中学2020年招聘教师2020-06-24 上海公务员考试《行测》通关模拟试题及答案解析【2019】:952020-06-12
上海公务员考试《行测》通关模拟试题及答案解析【2019】:952020-06-12 上海公务员考试《行测》通关模拟试题及答案解析【2019】:632020-06-12
上海公务员考试《行测》通关模拟试题及答案解析【2019】:632020-06-12 2019国考报名人数统计:铁路公安系统过审超6万 竞争力度较高【截至29日16时】2018-10-31
2019国考报名人数统计:铁路公安系统过审超6万 竞争力度较高【截至29日16时】2018-10-31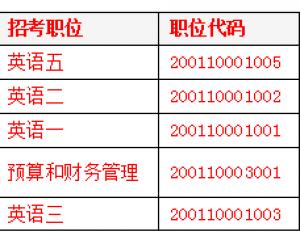 2019国考报名外交部过审3万余人 平均7人争一职2018-10-31
2019国考报名外交部过审3万余人 平均7人争一职2018-10-31