2017年9月15日由教育部考试中心的发布的2018年硕士研究生入学统一考试大纲已经与大家见面,考生最关心的考试大纲当中的考试内容与考试要求没有任何变化。
试卷结构和分值与往年相同,那么高等数学还是依然占有最重要的分值。历年来,很多同学觉得高等数学复习总是最难,那么下面我对高数的复习做几点说明:
一、多练习计算,注意计算题的方法和技巧。
高等数学的计算量是很大的,尤其是高等数学下册,那么计算的准确率就关系到你考研分数的高低,所以多练习计算是非常必要的。首先,对于客观题的计算题,要仔细,并且多总结一些技巧。对于客观题,很多题目都有很好的技巧,如果掌握了这些技巧,考试的时候会起到事半功倍的效果,节省不少时间来做解答题,所以在现在的复习过程中,就要常总结这些技巧。
再次,对于解答题的计算,通常方法是十分固定的。比如对于多元函数微分学那部分,求偏导数和全微分的题目,或者求极值、最值的问题,都是计算方法十分固定的,像这类题目,只要平时掌握好计算方法并加以练习,那么在考研的时候往往都是能拿满分的。对于某些题目的计算,比如数一和数三要求的级数的那部分,求幂级数的和函数,这种题目的计算需要非常仔细,一般计算量会比较大,并且容易出错,那么就需要大家在平时练习时弄明白这种题型每一步是什么原因,自己会写整个题目过程,项数的变换、求导、求积分该注意的问题需要非常清楚,时刻保持清晰的头脑。
计算的正确率是需要平时练习的,不要指望最后考试的时候仔细,仔细不是考试带给你的,是你的习惯。所以现在开始大家就要仔细做好每一步的计算,这里不得不说的是,有个别字差的同学需要练练字了,不然考研的时候改卷老师看不懂你的答案那就比较可惜了。
二、对于高等数学的证明题目,需要总结归纳常用方法。
考研数学会出现1-2道证明题,一般高数会出现一道证明。这类证明题一般在微分中值定理和导数的应用这部分考察。
对于证明题,很多同学感觉比较棘手,其实证明题的思路和方法也是比较固定的。比如微分中值定理的证明,如果是只含中值的等式,那么考虑罗尔定理,这里需要重点掌握构造辅助函数的方法;而对于既含中值也含端点值的等式,需要考虑拉格朗日中值定理或者柯西中值定理,那么两个方法要对照一下,看他们的区别与联系,把结论形式转化成定理的标准形式,对照定理结果就能确定是哪个定理,所以这两个定理的使用是不会混淆的。
对于导数的应用,无非是要用到求一阶导二阶导,判断单调性和极值、最值,这样可以证明函数的不等式或者常数的不等式。
所以对于证明题的方法只要总结归纳到位,在考研的时候就不会措手不及了。大家千万不要抱侥幸心理,觉得我只需要掌握某些类型,其他类型不会考。在考研的时候,只要是大纲要求的,就有可能考到,所以对于常见的题型和方法,一定要在进考场前就烂熟于心。
更多精彩资讯请关注查字典资讯网,我们将持续为您更新最新资讯!
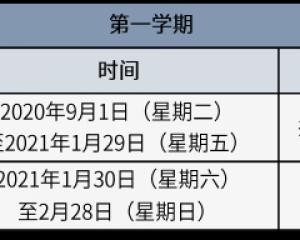 北京中小学8月29日起分批错峰开学 2021年1月30日放寒假-查字典资讯网2020-09-15
北京中小学8月29日起分批错峰开学 2021年1月30日放寒假-查字典资讯网2020-09-15
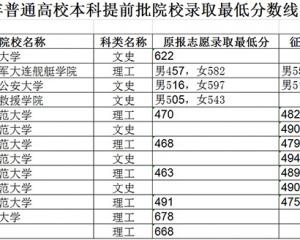 黑龙江:2020年普通高校本科提前批院校录取最低分数线-查字典资讯网2020-08-19
黑龙江:2020年普通高校本科提前批院校录取最低分数线-查字典资讯网2020-08-19 交叉学科将成第14个门类,这些高校早已抢占先机!2020-08-10
交叉学科将成第14个门类,这些高校早已抢占先机!2020-08-10 2021考研招生简章已公布?汉族考生也可享受“少干计划”的降分优惠?-查字典资讯网2020-08-06
2021考研招生简章已公布?汉族考生也可享受“少干计划”的降分优惠?-查字典资讯网2020-08-06